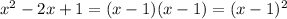Question

I would greatly appreciate if someone could explain this to me!

Answer 1

Remember that, in general, a quadratic equation can be written as:

`ax^2+bx+c`

In our problem, we already have the values of a and b, c is the missing value. When this happens, that a and b are given, the value of c is equal to:

`c=((b)/(2))^2`

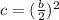
Therefore, the missing value in the problem is:

`\begin{gathered} b=-2 \\ \Rightarrow c=(-(2)/(2))^2=(-1)^2=1 \\ \Rightarrow c=1 \end{gathered}`

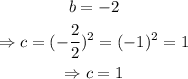
Thus, the answer is 1

We can easily verify that this answer is correct as follows:

`x^2-2x+1=(x-1)(x-1)=(x-1)^2`