Question

7. Consider the product (3x+1)^2(a) Write this product in standard trinomial form.(b) Use your answer in part (a) to determine thevalue of 31^2 without your calculator.

Answer 1

(a)

We will use

`(a+b)^2`

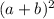
formula to expand this.

The formula is

`(a+b)^2=a^2+2ab+b^2`

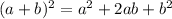
In the question, a is 3x and b is 1

Thus,

`\begin{gathered} \left(3x+1\right)^2=(3x)^2+2(3x)(1)+(1)^2 \\ =9x^2+6x+1 \end{gathered}`

(b)

The trick here is to put "31" somehow being into the form (3x+1), so that we can use the formula from part (a).

So, what value in "x" would make (3x+1) into 31?? Simple! x = 10!

How?

`\begin{gathered} 3x+1=31 \\ 3x=31-1 \\ 3x=30 \\ x=10 \end{gathered}`

So, for x = 10, 3x+1 becomes "31", so 31^2 would be simply putting x = 10 into the answer (expanded) form of part (a).

So,

`\begin{gathered} 9x^2+6x+1 \\ 31^2=9(10)^2+6(10)+1=9(100)+60+1=900+61=961 \end{gathered}`

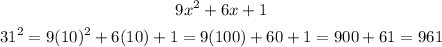
Part (b) is 961