Part (a)
The momentum along x- direction of the system before the collision is given as,
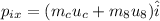
Here, m_c is the mass of cue ball (m_c=0.6 kg), u_c is the initial velocity of cue ball (u_c=2 m/s), m_8 is the mass of eight ball (m_8=0.6 kg), and u_8 is the initial velocity of the eight ball (u_8=0 m/s, as the eight ball was initally at rest).
Substituing all known values,
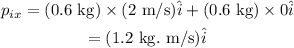
The momentum along y- direction of the system is given as,
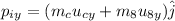
Here, u_cy is the y-component of velocity of cue ball along y direction (u_cy=0) and u_8y is the y-component of velocity of eight ball along y direction (u_8y=0).
Substituting all known values,
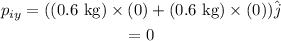
Therefore, the momentum of the system in vector form is,
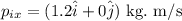
Part(b)
According to law of conservation of momentum, the momentum before and after the collision remains same. Therefore, the momentum of the system after the collison remain same.
Part (c)
The x-component of the velocity of the cue ball after collision is given as,

Here, v_c is the component of the cue ball after collision (v_c=0.8 m/s) and θ is the angle it makes with horizontal (θ=20°).
Substituting all known values,
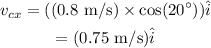
The y-component of velocity is given as,

Substituting all known values,
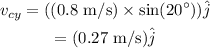
Therefore, the velocity of cue ball after the collision in vector form is,
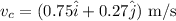
Part (d)
Applying conservation of momentum along x-direction.
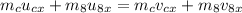
Here, v_8x is the x component of the velocity of eigth ball after collision.
Substituting all known values,
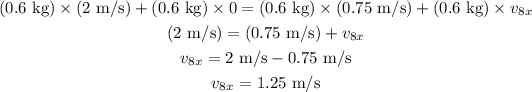
Part (e)
Applying conservation of momentum along y-direction.
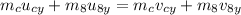
Here, v_8y is the y-component of velocity of the eight ball after collision .
Substituting all known values,
![\begin{gathered} (0.6\text{ kg})*0+(0.6\operatorname{kg})*0=(0.6\text{ kg})*(2.7\text{ m/s})+(0.6\text{ kg})* v_(8y) \\ 0=2.7\text{ m/s}+v_(8y) \\ v_(8y)=-2.7\text{ m/s} \end{gathered}]()