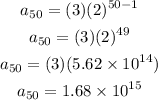Question

3 6 12 24 50th term.

Answer 1

Geometric sequences is a sequence of numbers where each term after the first is found by multiplicatying the previous by a common ratio, and is given by the expression:

`a_n=a_1r^(n-1)`

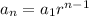
an= the term we want to find

a1= the first term of the sequence

n= the position of the term

r= ratio is the cocient between two consecutive pairs

r=6/3=2

r=12/6=2

So, the 50th term would be:

`\begin{gathered} a_(50)=(3)(2)^(50-1) \\ a_(50)=(3)(2)^(49) \\ a_(50)=(3)(5.62*10^(14)) \\ a_(50)=1.68*10^(15) \end{gathered}`