Question

An object with mass m is suspended at rest from a spring with a spring constant of [k] N/m. The length of the spring is x1 cm longer than its unstretched length L, as shown above. A person then exerts a force on the object and stretches the spring an additional x2 cm. What is the total energy stored in the spring at the new stretched length? m = 154.498 K = 155 x1 =22 L = 27 x2 = 17

Answer 1

Answer:

The energy stored in the spring = 11.79 Joules

Step-by-step explanation:

The energy stored in a spring is given by the formula:

`E=(1)/(2)kx^2`

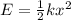
where E is the energy

k is the spring constant

x is the extension

The length of the spring is extended by x₁ and x₂

The energy stored in the spring is therefore:

`E=(1)/(2)k(x_1+x_2)^2`

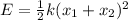
x₁ = 22 cm

x₁ = 22/100

x₁ = 0.22 m

x₂ = 17 cm

x₂ = 17/100

x₂ = 0.17 m

The spring constant, k = 155 N/m

Substitute x₁ = 0.22 m, x₂ = 0.17 m, and k = 155 N/m into the formula for the energy. The energy stored in the spring is therefore calculated as follows

`\begin{gathered} E=(1)/(2)(155)(0.22+0.17)^2 \\ E=0.5(155)(0.1521) \\ E=\text{ 11.79J} \end{gathered}`

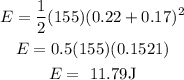
The energy stored in the spring = 11.79 Joules