Question

two sides of a triangle have the measures of 12 and 10. find the range of possible measures for the third sideA. 10

Answer 1

Given that,

The two sides of a triangle have measures 12 and 10.

We have to determine,

The range of possible measures for the third side.​

According to the question,

To find the range of the third side of the triangle by using the triangle inequality theorem.

Let, the third side of the triangle be x.

Then, by the triangle inequality theorem, we have the following three true statements.

`\begin{gathered} x+12>10 \\ x+10>12 \\ 10+12>x \end{gathered}`

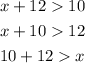
These three statements come from the fact that the sum of any two sides of a triangle must sum to a length greater than the length of the third side of the triangle.

Solve the inequality for the value of x in all three of the inequalities.

`\begin{gathered} x>-2 \\ x>2 \\ 22>x \end{gathered}`

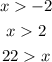
All three of these must be true at the same time.

That is x>2, x>−2, and x<22.

Two of these statements can be compressed into one, though. For, if x>2 and x>−2, we can just say that x>2, because that accounts for both of those inequalities.

There are 2 terms left with only two statements. x>2 and x<12, which can be written as,

[tex]2Hence, The range of possible measures for the third side is between 2 and 22.

The correct option