Question

DFor each question, construct a normal distribution curve and label the horizontal axis. Then answer eachquestion.10+11. The mean life of a tire is 30 000 km. The standard deviation is 2000 km.a) 68% of all tires will have a life betweenkm andkm.km.b) 95% of all tires will have a life betweenkm andc) What percent of the tires will have a life that exceeds 26 000 km?ad) If a company purchased 2000 tires, how many tires would you expect to last more than 28 000 km?

Answer 1

The normal distribution curve is as shown;

Given:

`\begin{gathered} \mu=30,000km \\ \sigma=2000km \end{gathered}`

Question a:

If 68% of all tires will have a life when the Z-score is between -1 and 1.

Hence,

when Z = -1

`\begin{gathered} \\ Z=(x-\mu)/(\sigma) \\ -1=(x-30000)/(2000) \\ Cross\text{ multiplying;} \\ -1(2000)=x-30000 \\ -2000=x-30000 \\ -2000+30000=x \\ x=30000-2000 \\ x=28000km \end{gathered}`

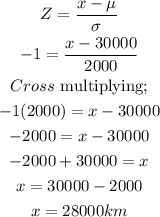
when Z = 1

`\begin{gathered} \\ Z=(x-\mu)/(\sigma) \\ 1=(x-30000)/(2000) \\ Cross\text{ multiplying;} \\ 1(2000)=x-30000 \\ 2000=x-30000 \\ 2000+30000=x \\ x=30000+2000 \\ x=32000km \end{gathered}`

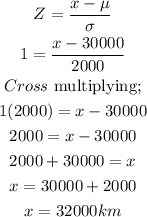
Therefore, 68% of all tires will have a life between 28,000km and 32,000km.

Question b:

If 95% of all tires will have a life when the Z-score is between -2 and 2.

Hence,

when Z = -2

`\begin{gathered} \\ Z=(x-\mu)/(\sigma) \\ -2=(x-30000)/(2000) \\ Cross\text{ multiplying;} \\ -2(2000)=x-30000 \\ -4000=x-30000 \\ -4000+30000=x \\ x=30000-4000 \\ x=26000km \end{gathered}`

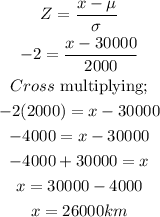
when Z = 2

`\begin{gathered} \\ Z=(x-\mu)/(\sigma) \\ 2=(x-30000)/(2000) \\ Cross\text{ multiplying;} \\ 2(2000)=x-30000 \\ 4000=x-30000 \\ 4000+30000=x \\ x=30000+4000 \\ x=34000km \end{gathered}`

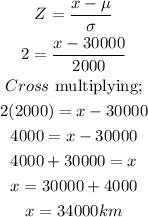
Therefore, 95% of all tires will have a life between 26,000km and 34,000km.

Question c:

The percent of tires that will have a life that exceeds 26,000km is;

`\begin{gathered} Z-score\text{ when x = 26000} \\ Z=(x-\mu)/(\sigma) \\ Z=(26000-30000)/(2000) \\ Z=-(4000)/(2000) \\ Z=-2 \end{gathered}`

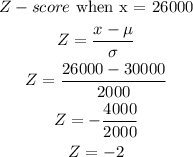
From Z-score tables,

`\begin{gathered} P(x>Z)=0.97725 \\ As\text{ a percent,} \\ 0.97725*100=97.725 \\ \approx97.73 \end{gathered}`

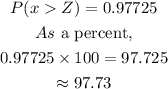
Therefore, the percent of tires that will have a life that exceeds 26,000 is 97.73%

Question d:

The probability of tires that will have a life that will last more than 28,000km is;

`\begin{gathered} Z-score\text{ when x = 28000} \\ Z=(x-\mu)/(\sigma) \\ Z=(28000-30000)/(2000) \\ Z=-(2000)/(2000) \\ Z=-1 \end{gathered}`

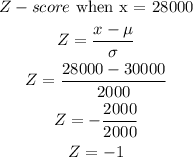
From Z-score tables,

`P(x>Z)=0.84134`

Hence, the number of tires that would last more than 28000km if the company purchased 2000 tires will be;

`\begin{gathered} E=n.P(x) \\ E=2000*0.84134 \\ E=1682.68 \\ E\approx1683\text{ tires to the nearest whole number.} \end{gathered}`

Therefore, the number of tires that would last more than 28,000km if the company purchased 2000 tires will be approximately 1,683 tires to the nearest whole number.