Here, we want to use geometry to show that the pre-image segemnt is parallel to the image segment
The pre-image segment is A (-4,4) and (8,8) while the image segment after dilating using the origin as the center and a scale factor of 1/2 is A' (-2,2) and B' (4,4)
Now, according to geometry, if the two segments are parallel, then their slopes must be equal.
We proceed to find the slope of both segments
The general equation to find the slope of a line segment is;
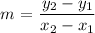
For segment AB, we have;
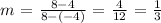
For the image segment A'B' we have;
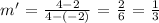
As we can see from above, the slope of the two line segments are equal
i.e;
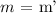
This concludes that both line segments are parallel since their slopes are of equal magnitude