The number of surveyed teachers who play videogames is 6, according to the table; therefore,
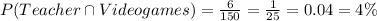
On the other hand, if A and B are two independent events,
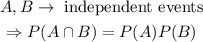
Thus, in our case,
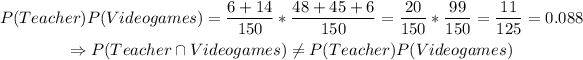
Therefore, the two events are not independent.
Hence, the answer is the first option, 4%, and not independent.