Question

In Circle A as shown Below,segment DC IS tangent to Circle A at D. Also,DC=4 and BC=2.Find the length of the radius of Circle A ?

Answer 1

Given the circle A

As shown :

DC is tangent to the circle

AD is the radius of the circle

so, AD will be perpendicular to the radius

Let AD = r

so,

`\begin{gathered} AD=r \\ DC=4 \\ AC=AB+BC=r+2 \end{gathered}`

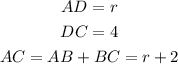
The triangle ADC is a right triangle

Using the Pythagorean theorem:

`\begin{gathered} AC^2=AD^2+DC^2 \\ (r+2)^2=r^2+4^2 \end{gathered}`

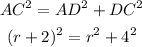
solve the equation to find r:

`\begin{gathered} r^2+4r+4=r^2+16 \\ 4r=16-4 \\ 4r=12 \\ \\ r=(12)/(4)=3 \end{gathered}`

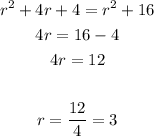
So, the answer will be:

The radius of the circle A = 3