We need to determine whether the functions below are inverses of each other:
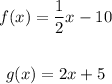
When two functions F and G are inverses of each other, they satisfy the following result:
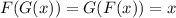
So, let's check whether the given functions are inverses of each other:
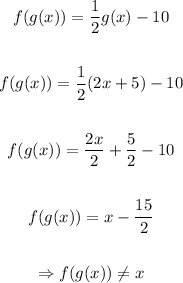
Therefore, the given functions are not inverses of each other.