1 Answer

Michael Vincent · Answer 1 · 2023-09-24T13:34:22+0000

We have to calculate the number of data within 2 population standard deviation of the mean.

For we have to find the mean of the given data.

Mean is given by

$\operatorname{mean}=(87+63+39+67+66+63+62+67+66)/(9)=(580)/(9)=64.44$

The standard deviation is given by the formula,

$\sigma=\sqrt[]{\frac{\Sigma(x_i-\operatorname{mean})^2}{9}}$

Then the standard deviation is given by

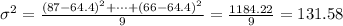
$\sigma^2=\frac{(87-64.4)^2+\cdots+(66-64.4)^2^{}}{9}=(1184.22)/(9)=131.58$

Hence the standard deviation is

$\sigma=\sqrt[]{131.58}=11.47$

Please log in or register to add a comment.