Given:
The number of petunias and daffodils planted by 3 neighbors.
We will find the ratio of petunias to daffodils for each one:
The ratio of petunias to daffodils for mra. H =
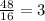
The ratio of petunias to daffodils for mrs M =
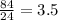
The ratio of petunias to daffodils for mrs P =
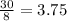
We will choose the greatest ratio
So, the answer will be option C. mrs. p