Question

Reaction C3H8(g) + 5O2(g) --> 3CO2(g) + 4H2O(g)If a scientist completely reacts 492.3grams of oxygen gas (O2) with excess propane (C3H8), how many particles, in moles, of carbon dioxide is likely to form? (Round any atomic masses on the periodic table to one decimal place.)

Answer 1

`\text{ 5.5567 }*\text{ 10}^(24)\text{ particles}`

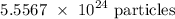
Step-by-step explanation

Given that:

The mass of oxygen is 492.3 grams

Follow the steps below to find the number of particles of CO2

Step 1; Write the balanced equation of the reaction

`\text{ C}_3H_(8(g))\text{ + 5O}_(2(g))\text{ }\rightarrow\text{ 3CO}_(2(g))\text{ + 4H}_2O_((g))`

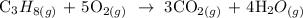
Step 2; Find the number of moles of oxygen using the formula below

`\text{ mole = }\frac{\text{ mass}}{\text{ molar mass}}`

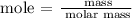
Recall, that the molar mass of oxygen is 32 g/mol

`\begin{gathered} \text{ mole = }\frac{\text{ 492.3}}{\text{ 32}} \\ \text{ mole = 15.384 moles} \end{gathered}`

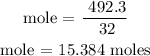
Step 3; Find the number of moles of CO2 using a stoichiometry ratio

5 moles O2 give 3 moles CO2

Let moles of CO2 be x

`\begin{gathered} \text{ 5 moles O}_2\text{ }\rightarrow\text{ 3 moles CO}_2 \\ \text{ 15.384 moles O}_2\text{ }\rightarrow\text{ x moles CO}_2 \\ \text{ Cross multiply} \\ \text{ 5 moles O}_2\text{ }*\text{ x moles CO}_2\text{ = 3 moles CO}_2*15.384\text{ moles O}_2 \\ \text{ Isolate x} \\ \text{ x = }\frac{\text{ 3moles CO}_2*15.384moles\cancel{O_2}}{5moles\cancel{O_2}} \\ \text{ x = }\frac{\text{ 3 }*\text{ 15.384}}{5} \\ \text{ x =}(46.152)/(5) \\ \text{ x = 9.2304 moles} \\ \text{ Therefore, the number of moles of CO}_2\text{ IS 9.2304 moles} \end{gathered}`

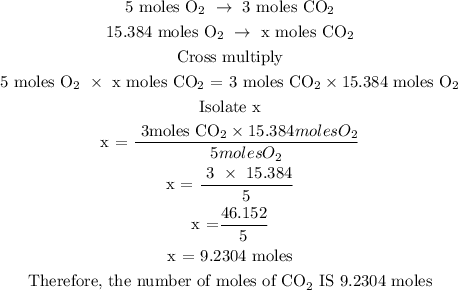
Step 4; Find the number of particles of CO2 using the formula below

`\begin{gathered} \text{ mole = }\frac{\text{ number of particles}}{\text{ Avogadro's number}} \\ \text{ } \end{gathered}`

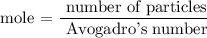
Recall, that the Avogadro's constant is 6.02 x 10^23

`\begin{gathered} \text{ 9.2304 = }\frac{\text{ number of particles}}{\text{ 6.02 }*\text{ 10}^(23)} \\ \text{ cross multiply} \\ \text{ Number of particles = 9.2304 }*\text{ 6.02 }*\text{ 10}^(23) \\ \text{ Number of particles = 55.567 }*\text{ 10}^(23) \\ \text{ Number of particles = 5.5567 }*\text{ 10}^(24)\text{ particles} \\ \text{ Therefore, the number of particles of CO}_2\text{ is 5.5567 }*\text{ 10}^(24)\text{ particles} \end{gathered}`