We need to graph the next function:
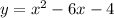
This is a parabola, and we need 3 points to graph it.
The x-coordinate of a parabola is computed as follows:
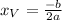
where a and b are the coefficients of the parabola. Substituting with a = 1, and b = -6, we get:
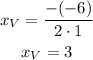
The y-coordinate of the vertex is found substituting xV into the equation as follows:
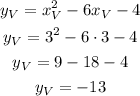
The vertex is the point (3, -13)
Substituting x = 2 into the equation of the parabola, we get:
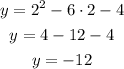
Substituting x = 4 into the equation of the parabola, we get:
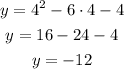
Then, the parabola passes through the points (2, -12) and (4, -12). Connecting these points and the vertex, we get the next graph:
The line y = 3 is shown in green.
From the graph, we can see that the parabola (x²-6x-4, in blue) is greater than 3 (in green) for the next values of x:
x < -1 or x > 7