Question

Use the following isosceles triangle to find valur of x and the length of ac.

Answer 1

Given that the triangle is isosceles, we can say that AB = AC. Using the given expressions we can form the following equation.

`\begin{gathered} AB=AC \\ 5x+8=7x-6 \end{gathered}`

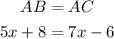
Let's solve for x.

`\begin{gathered} 8+6=7x-5x \\ 14=2x \\ x=(14)/(2) \\ x=7 \end{gathered}`

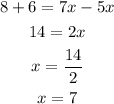
Once we have the value of the variable, we can find the length of AC.

`\begin{gathered} AC=7x-6 \\ AC=7(7)-6 \\ AC=49-6 \\ AC=43 \end{gathered}`

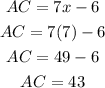
Therefore, the length of AC is 43.