Given:
Driver's license test scores for 2,000 high school students were normally distributed
The mean = μ = 80
And, the standard distribution = σ = 4
We will find the percentage of students who scored between 76 and 88
We will use the z-score to find the answer

So, the values of (z) when x = {76, 88} will be as follows:
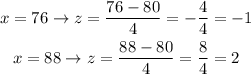
We will use the following chart to find the probability between -1 and 2
So, as shown, the probability will be:
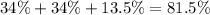
So, the answer will be option 3) 81.5%