The side length of the square, a=4.
An equilateral triangle has equal sides. Since the base of the triangle is one side of the square, we get
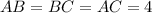
Since BQ⊥AC, BP is perpendicular to AC, and hence, BP is the altitude the equilateral triangle ABC.
The altitude BP of the equilateral triangle ABC is,
![\begin{gathered} BP=\frac{\sqrt[]{3}}{2}a \\ BP=\frac{\sqrt[]{3}}{2}*4 \\ BP=3.464 \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7bbdhm2ev79tgo4dmpqlhgicqmgmwf3tln.png)
Also, since BQ⊥ED, BQ⊥AC and P is midpoint of AC, Q is midpoint of ED.

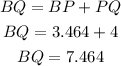
Now using Pythagoras theorem in triangle BQE,
![\begin{gathered} BE=\sqrt[]{BQ^2+EQ^2} \\ BE=\sqrt[]{(7.464)^2+2^2} \\ BE=7.7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uy854dks0lmzpihj5kcieotb3s2wrmpx0b.png)
Therefore, BE=7.7.