The solutions to the equation
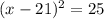 are:
are:
1.
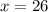
2.
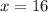
To solve the equation
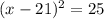 , we will use the square root property, which states that if
, we will use the square root property, which states that if
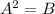 , then
, then
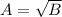 or
or
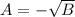 . Here are the steps for the calculation:
. Here are the steps for the calculation:
1. Take the square root of both sides of the equation:
![\[ √((x - 21)^2) = \pm √(25) \]](https://img.qammunity.org/2023/formulas/mathematics/college/ch88kdj9b1sdib74kvl18f6hnj0vcr9ilm.png)
2. Simplify both sides:
![\[ x - 21 = \pm 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/wpw1ias688hazcl8ossr44zbevqixbp3xh.png)
3. Solve for
 by adding 21 to both sides of the equation for each case:
by adding 21 to both sides of the equation for each case:
![\[ x = 21 \pm 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/37iy5x7wrwinn9qq4nljixmwa0fo713fmh.png)
This yields two solutions:
![\[ x = 21 + 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/sd9ourpubfksbcx8lappg2ap7hj2fwhdo2.png)
![\[ x = 21 - 5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/cj7sd99v5yx6o26c063q3i8yfxcmh7ouxf.png)
Now, let's calculate the exact values for \( x \).
The solutions to the equation
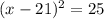 are:
are:
1.
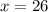
2.
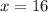
These are the two values of
 when plugged into the equation that will satisfy it.
when plugged into the equation that will satisfy it.