the area of the shaded region is 14.43 square units
Step-by-step explanation
to solve this we need to subtrac the area of a half circle from the area of the rectangle, so
Step 1
find the areas
a) rectangle
the area of a rectangle is given by:
note that thewidth of the rectangle equals the diameter of the circle, so

b)half circle
the area of half circle is given by:

so, let
diameter = 2
and replace
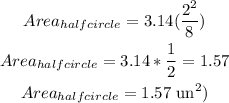
Step 3
finally, subtract the areas, so
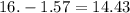
so, the area of the shaded region is 14.43 square units
I hope this helps you