At year 0, the value of the investment is $1400.
After 1 year, we have to add 9% to the previous value, that is,
1400 + 1400*0.09 = 1400(1 + 0.09) = 1400(1.09) = 1526
After the second year, we have to add 9% to the previous value, that is,
1526 + 1526*0.09 = 1526(1 + 0.09) = 1526(1.09) = 1400(1.09)(1.09) = 1400(1.09)²
Following the same reasoning, after t years the function will be:
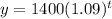
If t = 25, then:
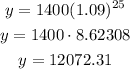
The value of the investment after 25 years will be $12,072.31