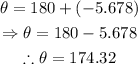Question

I am confused about this pre-calculus question. I only need to answer part B

Answer 1

Given that the airplane flies at 460 mph on a bearing of 170°, and a wind blows at 80 mph on a bearing of 200°. This is illustrated below:

A) Component of the velocity of the airplane.

Let the respective vertical and horizontal components of the plane be

`\begin{gathered} v_{y\text{ }}and_{}_{} \\ v_x \end{gathered}`

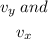
The vertical component of the airplane is evaluated as

`\begin{gathered} v_y=V\sin \theta=460*\sin 170 \\ =460*0.1736481777 \\ _{}=79.87816173 \\ \Rightarrow v_y=79.88 \end{gathered}`

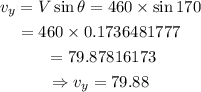
The horizontal component of the airplane is evaluated as

`\begin{gathered} v_x=V\cos \theta=460*\cos 170 \\ =460*(-0.984807753) \\ v_x=-453.01 \end{gathered}`

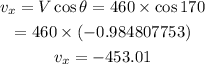
B) Actual ground speed and direction of the airplane.

The horizontal and vertical components of the wind is evaluated as

`\begin{gathered} \text{horizontal component: w}_x=W\cos \theta=80*\cos 200 \\ =80*(-0.9396926208) \\ w_x=-75.18 \\ \text{vertical component: w}_y=W\sin \theta=80*\sin 200 \\ =80*(-0.3420201433) \\ w_y=-27.36 \end{gathered}`

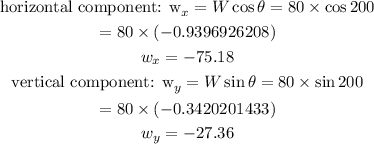
The velocity vector is thus expressed as

`\begin{gathered} V+W \\ =(v_x+v_y)+(w_x+w_y) \\ \text{collect like terms,} \\ =(v_x+w_x)+(v_y+w_y) \\ =(-453.01+(-75.18))+(79.88_{}+(-27.36)) \\ =(-528.19,\text{ 52.52)} \end{gathered}`

Actual speed:

Actual speed is evaluated as

`\begin{gathered} \sqrt[]{(-528.19)^2+(52.52)^2} \\ =\sqrt[]{278984.6761+2758.3504} \\ =\sqrt[]{281743.0265} \\ \Rightarrow=530.79\text{ mph} \end{gathered}`

Actual direction:

`\tan ^(-1)(\frac{vertival\text{ component of sp}eed}{horizontal\text{ component of sp}eed})`

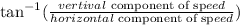
thus,

`\begin{gathered} \tan ^(-1)((52.52)/(-528.19)) \\ =\tan ^(-1)(-0.09943) \\ =-5.678 \end{gathered}`

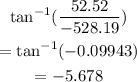
Hence, the direction becomes

`\begin{gathered} \theta=180+(-5.678) \\ \Rightarrow\theta=180-5.678 \\ \therefore\theta=174.32\degree \end{gathered}`