We can answer this question as follows:
We have that the clothing store is on sale and is selling pants, p, for $8.99, and shirts, s, for $3.99, and that we can spend no more than $60 (as much as $60).
We need to buy at least two pairs of pants.
Then, the system of inequalities is:
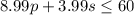
And at least two pairs of pants
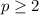
We can solve this system of inequalities graphically as follows:
And we can see that the darkest region is the region of the possible answers to our question. If we see the region, we can have the following answers:
If we buy 5 pants, and 3 shirts, we have (x for pants and y is for shirts):

Then
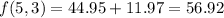
[Notice that the solutions must be for positive values for shirts (the possible negative solutions for y are nonsense in this situation: a negative value for a shirt?).]
Therefore, we can say that the latter is a possible solution since we spend less than $60 and we buy 5 pairs of pants and 3 shirts.
The other answer could be 3 pairs of pants and 8 shirts:

And also other answers are possible as this one:

In summary, we have that after solving the system of inequalities, we have that we can buy:
• Five, ,pants, and ,three, ,shirts, (,5 pants, 3 shirts,)
,
• Three pants, and ,eight shirts, (,3 pants, 8 shirts,)
And also
• Four pants, and ,five shirts, (,4 pants, 5 shirts,), and so on.
[The key in this exercise is to graph the system of inequalities and then find, in the shaded area in which both inequalities form a dark region, the possible values for the solution of the system.]