Given:
The equation is,
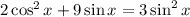
Step-by-step explanation:
Simplify the equation by using trigonometric identity.
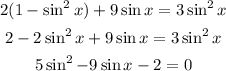
Assume sin x = t, then
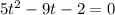
Solve the equation by splitting the middle term.
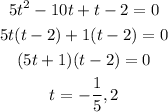
So,
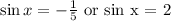
There is no possible value of x, for sin x = 2.
Determine the value of x by using sin x = -1/5.
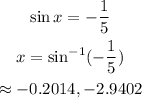
So possible values of x are -0.2014 and -2.9402.