Solution:
Given:

Rewriting the equations of the lines given in the slope-intercept form to get the slopes of the lines;

Also, for line 2

Two lines are perpendicular when the product of their slopes is -1.
Hence,

Multiplying the slopes of the two lines gotten;
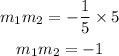
Since the product of their slopes is -1, then the two lines are perpendicular.