Question

the function f(x) = x^2 has been transformed, resulting in function g.function g is a ___ (horizontal translation/vertical translation/ dilation/ reflection) of function f.g(x) = ___(2|4| 1/4 | -1/4) x^2

Answer 1

Notice that the vertex of the graph of g(x) is at (0,0); therefore, no translation was applied to f(x). On the other hand, the graph of g(x) goes through (2,1) rather than (1,1); therefore, g(x) is a vertical compression of f(x).

In general, a vertical compression is given by the formula below (given a function h(x))

`h(x)\rightarrow ah(x);0Then, in our case,[tex]g(x)=a*f(x)`

To determine a, remember that the graph of g(x) includes the point (2,1); then,

`\begin{gathered} 1=g(2)=a*f(2)=a*2^2 \\ \Rightarrow1=a*4 \\ \Rightarrow a=(1)/(4) \\ \Rightarrow g(x)=(1)/(4)f(x) \end{gathered}`

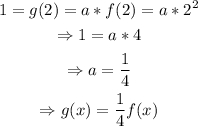
The answer is 'g(x) is a vertical compression of function f. g(x)=1/4*x^2'