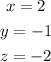We can isolate the variable x from the last equation by subtracting -6y and adding 8z to both sides, that is,

Now, we can substitute this result into the first and second equations. It leads,

By distributing the numbers into the parentheses, we have
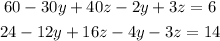
By collecting similar terms, we have
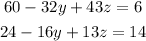
Now, by moving the number 60 to the right hand side of first equation and the number 24 to the right hand side of the second equaton, we have
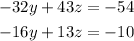
Now, let's isolate the variable y from the second equation. It yields,
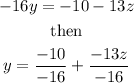
which gives
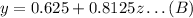
Now, we can substutite this result into the first equation (-32y+43z=-54), that is,
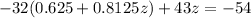
which gives

or equivalently,
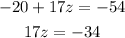
then
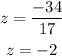
So, we have obtained the firs result z=-2. In order to find y, we can substitute our last result into equation (B) from above and get
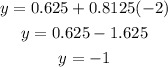
and by substituting z=-2 and y=-1 into equation (A), we have
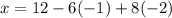
which gives
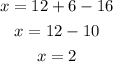
Therefore, the solution of the system is: