Question

On a number line, the line segment from Q to S has endpoints Q at -28and S at -46. Point R partitions the line segment from Q to Sin a 7:9ratio. What is the location of point R. Round to the nearest hundredthif necessary

Answer 1

If we follow the construction, we get the following picture

We want to determine the position of R to fullfill the given condition. First, let x the be the distance from Q to R, and let y be the distance from R to S. At a first glance, the sum of x and y should add up to the total distance between S and Q. To calculate the distance between Q and S, we simply subtract the position of Q and the position of S. In our case the total distance is

`\text{ - 28 - (46 ) = 46 -28 = 18}`

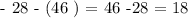
So, in our notation, we get the equation

`x+y\text{ = 18}`

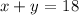
On the other hand we are told that the point R divides the segment in a 7:9 ratio. That is, the ratio of the distance from Q to R (x) and the distance from R to S (y) is 7:9. That is

`(x)/(y)=\text{ }(7)/(9)`

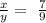
We can arrange this equation as

`9x\text{ = 7y}`

Now, consider the first equation we got (x+y=18). If we multiply both sides by 7, we get

`7\cdot(x+y)\text{ = 7x+7y = 18}\cdot7\text{ = }126`

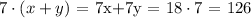
From the seconde equation, se have 7y = 9x, so if we replace this value, we get

`7x\text{ + (9x) = 126 = 16x}`

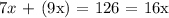
If we divide by 16 on both sides we get

`x\text{ = }(126)/(16)\text{ = }7.875`

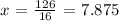
Now, since 7.875 is the distance from Q to R, we know that if we subtract the coordinates of Q and R, we should get 7.875

Then, let h be the position of R. So we have the equation

`\text{ -28 - h = 7.875}`

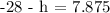
So, by adding by h on both sides and subtracting 7.875, we get

`\text{ - 28 - 7.875 = h = -35.875}`

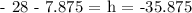
By rounding to the closest hundredth we get -35.88. So R is located at -35.88