Question

A certain disease has an incidence rate of 0.7%. If the false negative rate is 7% and the false positive rate is 4%, compute the probability that a person who tests positive actually has the disease.

Answer 1

Given:

The incidence rate of 0.7%.

The false-negative rate is 7%.

The false-positive rate is 4%.

To find:

The probability that a person who tests positive actually has the disease.

Step-by-step explanation:

Here, we have,

`\begin{gathered} P\mleft(disease\mright)=0.007 \\ P\mleft(Positive|disease\mright)=1-\text{False negative rate} \\ =1-0.07 \\ =0.93 \end{gathered}`

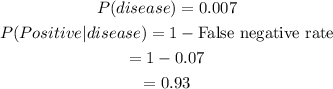
Let us find the probability of no disease.

`\begin{gathered} P(no\text{ }disease)=1-P(disease) \\ =1-0.007 \\ =0.993 \end{gathered}`

And since the false positive rate is 4%,

`\begin{gathered} P(Positive|no\text{ }disease)=\text{False positive rate} \\ =0.04 \end{gathered}`

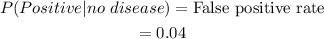
Using Bayes's theorem,

`P(disease|positive)=\fracdisease){P(disease)\cdot P(positive|disease)+P(no\text{ }disease)\cdot P(positive|no\text{ }disease)}`

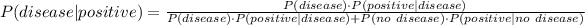
On substitution we get,

`\begin{gathered} P(disease|positive)=((0.007)(0.93))/((0.007)(0.93)+(0.993)(004)) \\ =(0.00651)/(0.00651+0.03972) \\ =(0.00651)/(0.04623) \\ =0.14081 \\ \approx0.141 \\ =14.1\text{ \%} \end{gathered}`

Final answer:

The probability that a person who tests positive actually has the disease is 0.141 or 14.1%