Question

Aaron just hopped on the edge of a merry-go-round. What are his linear and angular speeds if the diameter of the merry-go-round is 11 feet and it takes 7 seconds forit to make a complete revolution? Round the solutions to two decimal places.

Answer 1

Given:

Diameter = 11 feet

Time to complete one revolution = 7 seconds

Let's find the linear speed and angular speed.

To find the angular speed, apply the formula:

`w=(\Delta\theta)/(t)=(2\pi)/(t)`

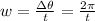
Where:

t = 7 seconds

Thus, we have:

`\begin{gathered} w=(2\pi)/(7) \\ \\ w=0.897\text{ rad/s }\approx\text{ 0.90 rad/s} \end{gathered}`

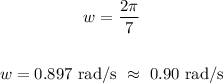
The angular speed is 0.90 rad/s.

To find the linear speed, apply the formula:

`v=rw`

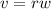
Where:

r is the radius

w is the angular velocity.

We have:

`\begin{gathered} v=(d)/(2)* w \\ \\ v=(11)/(2)*0.90 \\ \\ v=5.5*0.90 \\ \\ v=4.94\text{ ft/s} \end{gathered}`

The linear speed is 4.94 ft/s.

ANSWER:

w = 0.90 rad/s

v = 4.94 ft/s