There are many methods to solve a system of equations but let's discuss the methods stated in the question.
Graphing method.
To solve a system of equations by the graphing method we need to graph each of the equations on the plane. Once we do that we look for the intersection of the lines; the point where all the lines intersect is the solution to the sytem of equations. For example, the system of equations:
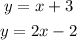
can be graph as:
the solution of the system is the intersection point; in this case this is the point (5,8). This means that the solution of the system is x=5 and y=8; to verify this we just need to plug the values in our system and we need to verify that both the equations hold for this values.
Plugging the values in the first equation we have:
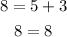
then the point satisfy the first equation.
Doing the same for the second equation we have that:
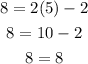
and once again the point we found satisfy the equation.
Now, the graphing method is useful when the equation are written in the slope-intercep form:

(Notice how the example is written in that form). This comes from the fact that this form already tells us where each of the lines intersect the y-axis and then we would only need to find another point for each line to graph them.
Substitution method.
The substitution method consist in the following steps:
0. Solve one equation for one of the variables.
,
1. Substitute the expression found in the previous step in the other equation.
,
2. Solve the equation found in the previous step.
,
3. Resubstitute the value found to the equation found in the first step to find the remaining variable.
Let's apply this method to the example in the graphing method, that is, the system:
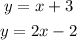
Since both of the equation are already solve for one of the variables we choose the first one to substitute in the second one, then we will have:
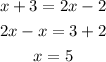
Now that we know the value of x we plug it in the first equation to find y:
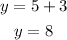
And therefore x=5 and y=8. (Notice how we got the same result, as we should).
The substitution method is best used when one of the equations is written in terms of one of the variables (like the equations in the system we use as an example)
Linear combination method (Elimination method).
The linear combination method consist in the following steps:
0. Arrange the equation with like terms in columns.
,
1. Analyze the coefficients of x or y. Multiply one or both equations by an appropriate number to obtain new coefficients that are equal or opposites.
,
2. Add or subtract the equations; then solve the resulting equation for the remaining variable.
,
3. Substitute the value of the variable found in either of the original equations and solve.
Let's apply this method for the example we are working with:
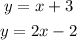
First we write the equation with like terms in columns:
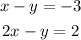
Now we notice that the coefficients of the variable y are equal; this means that we can subtract the equation to eliminate this variable. Let's subtract the second equation from the first, then we would have:
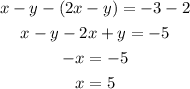
Once we know the variable x we plug its value in one of the equation to find y:
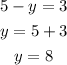
Therefore x=5 and y=8. (notice how, once again, we get the same result as the previous methods.)
This method is best used when the equations are written in the form we need from the beginning and when one of the coefficients of the variable is the same.
Note: All of the methods lead to the same result, as they must, this means that in reality there's no best method to solve a system of equations since all of them will lead to the same result. What we really do, in practice, is to use one of them when it is eaiser but this is subjective and some people might find easier one of the methods instead of the other.