Question

If the first of three Consecutive integers is subtracted from 111 the result is the sum of the second and third what are the integers

Answer 1

Let the consecutive integers be x, y, and z

Since the first integer "x" is subtracted from 111, that becomes

111 - x

Now, the result of subtraction is equal to the sum of the second and third. This becomes

111 - x = y + z

Since they are consecutive, it means that

y = x + 1 and z = x + 2

So

`\begin{gathered} 111-x=y+z \\ 111-x=(x+1)+(x+2) \\ 111-x=x+1+x+2 \\ \text{Collecting like terms we have } \\ 111-1-2=x+x+x \\ 108=3x \\ (108)/(3)=(3x)/(3) \\ \\ x=36 \end{gathered}`
`\begin{gathered} y=x+1 \\ y=36+1 \\ \\ y=37 \end{gathered}`
`\begin{gathered} z=x+2 \\ z=36+2 \\ \\ z=38 \end{gathered}`

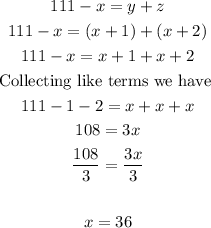
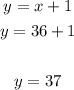
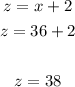
Therefore, the integers are 36, 37 and 38