Given
The function f(x) is defined as:

The zeros of a function are the values of x when f(x) is equal to 0.
Solving for the zeros:
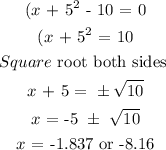
The vertex of the parabola is the point at which the function changes direction
First we take the derivative of f(x), set it to zero and then solve for x.
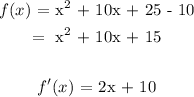
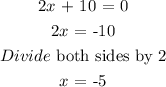
Next, we substitute the value of x into f(x):
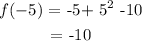
Hence, the vertex is (-5, -10)
Hence, the correct option is vertex is (-5, -10) (Option B)