Given the following expression:
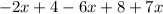
You need to remember the following definitions:
1. Terms are part of the expression. These are separated by one of these signs:

A term can be a variable or a number.
2. Like terms are those terms that have the same variables and the same exponents.
3. The coefficients are the numbers that multiply the variables.
4. The Constant term is the term that only shows the coefficient because its variable is:
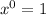
For example, let be "a" a coefficient:
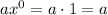
Knowing those definitions, you can identify that:
- In this case, the like terms of the expression are:
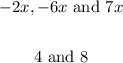
- These are coefficients:
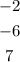
- And these are Constant terms:

Hence, the answer is:
- Like terms:
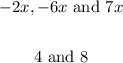
- Coefficients:
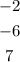
- Constant terms:
