Given point p and slope m, below
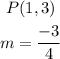
The formula for finding point slope point of a straight-line graph is given below
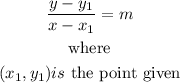
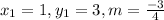
Substitute the given into the formula
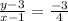
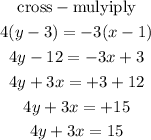
The graph is as shown below:
Hence, the slope-point form of the given point and slope is 4y+3x=15