Answer:
-1.22 m/s
Step-by-step explanation:
To find the initial velocity, we will use the following equation:
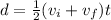
Where d is the displacement, t is the time, vi is the initial velocity and vf is the final velocity.
So, replacing vf by 7.8 m/s, t by 5.7s, and d by 18.75 m, we get:
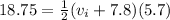
Now, we can solve for vi:

Therefore, the initial velocity of the bike was -1.22 m/s