Question

Here is a figure made of two rectangles.64 A736 ft125.ft48 Á(a) What is the area of the figure?square feetfeet(b) What is the perimeter of the figure?(c) How much greater is the area of the figure than its perimeter?

Answer 1

The figure is made of two rectangles. Hence, we can find the area when we add up both rectangles' areas.

The area of a rectangle is given by:

`A=Length\ast Width`

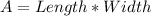
Area for the smaller rectangle:

`\begin{gathered} A=36ft\ast48ft \\ A=1728ft^2 \end{gathered}`

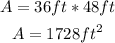
Area for the larger rectangle:

`\begin{gathered} A=64ft\ast125ft \\ A=8000ft^2 \end{gathered}`

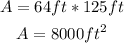
Finally, we need to add up both areas:

Atotal = 1728 ft² +8000ft² = 9728ft²

Hence, the area of the figure is 9728ft².

Now, to find the perimeter we need to add up all the sides of the figure.

Hence, We find the perimeter by adding the outsides edges of our shape.

P= 48ft +36ft + (125ft-48ft) +64ft + 125ft +(64ft+36ft)

P=450 ft

Now, the area of the figure is greater 21.6 times than the perimeter.