Question

Follow the process of completing the square to solve x^2 - 10x + 8 = 0. How will the left side of the equation factor in step 5?(x - 10)²(x - 20)²(2x - 10)²

Answer 1

In order to complete the square, since we have the term -10x, we need the term 5² = 25 to have a perfect square. So adding this term to both sides of the equation, we have:

`\begin{gathered} x^2-10x+8=0 \\ x^2-10x+25+8=25 \\ (x-5)^2+8=25 \\ (\mleft(2x-10\mright)^2)/(4)=17_{} \\ \mleft(2x-10\mright)^2=68 \end{gathered}`

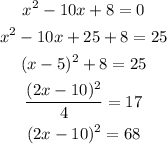
The left side of the equation is (2x - 10)², therefore the correct option is the third one.