The question represents a binomial distribution.
The binomial probability formula is calculated using the formula:
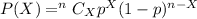
where
P = binomial probability
X = number of times for a specific outcome within n trials
n C x = number of combinations
p = probability of success on a single trial
n = number of trials
From the question, we have the following parameters:

We are to evaluate the probability that more than 5 and less than 9, hence:
![P(5<strong>At X = 6:</strong>[tex]\begin{gathered} P(6)=^(10)C_6\cdot0.3^6\cdot(1-0.3)^(10-6) \\ P(6)=0.0368 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9ule57k6fckpwnz9tz4kwfs337x9k1vdso.png)
At X = 7:
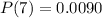
At X = 8:
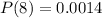
Therefore, the probability will be:
[tex]P(5
The probability is 0.0472.