Question

Find the sum of the first n terms of the sequence6,13,20,27,...;n=11

Answer 1

To find the sum of the first n terms we first need to find the expression for the sequence. We notice that this is an arithmetic sequence since the difference between each term is the same. In this case this difference is 7, then the sequence is:

`\begin{gathered} a_n=6+7(n-1) \\ a_n=6+7n-7 \\ a_n=7n-1 \end{gathered}`

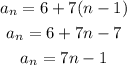
Now we need to remember that the sum of the first n terms in an arithmetic sequence is given as:

`S_n=(n(a_1+a_n))/(2)`

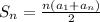
In this case n=11, then:

`\begin{gathered} S_(11)=(11(7(1)-1+7(11)-1))/(2) \\ S_(11)=(11(6+76))/(2)_{} \\ S_(11)=(11(82))/(2) \\ S_(11)=(902)/(2) \\ S_(11)=451 \end{gathered}`

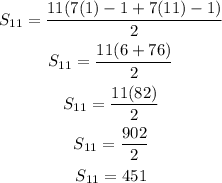
Therefore the answer is D