The kinetic energy in terms of the amplitude of oscillation is,
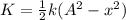
where k is the spring constant and x is the position,
The potential energy in terms of the amplitude of oscillation is,
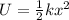
The value of position when the kinetic energy of the oscillation is 3 times the potential energy is,
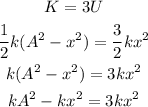
By simplifying,
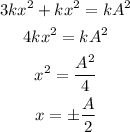
Thus, the position at which the kinetic energy becomes 3 times the potential energy is half of the amplitude.