We have a question about probability. Our approach is to obtain the mean amount that can be obtained for the possible outcomes.
Probability is derived as:

The probability, P of obtaining a white can be derived knowing:
# of desired outcome = 2
# of total outcome = 16

The average amount obtainable for spinning a white is:
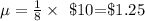
The probability, Q of obtaining any other color can be derived knowing:
# of desired outcome = 14
# of total outcome = 16
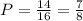
The average amount obtainable for spinning any other color is:

Net gain on average: Average amount gained - Average amount lost
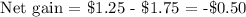
On average, the player loses 50 cents. That makes it unfavorable for him.
OPTION C