Question

Decide if the two lines y =1* - 4 and y = 8x + 6 are parallel, perpendicular, or neither. Explain your answer.Keypad

Answer 1

Step-by-step explanation

Before we can determine whether the lines are parallel or perpendicular, we must understand the conditions for the lines to be parallel pr perpendicular.

For two lines to be parallel, they must have the same slope and for the lines to be perpendicular, the product of their slopes must be -1.

The equation of a line in slope-intercept form is expressed according to the formula;

`y=mx\text{ +b}`

m is the slope of the line

Given the equation of the first line expressed as:

`\begin{gathered} y=(1)/(8)x-4 \\ m_1x=(1)/(8)x \\ m_1=(1)/(8) \end{gathered}`

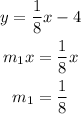
This shows that the slope of the line is 1/8

For the second line given as y = 8x + 6. The slope is given as;

`\begin{gathered} m_2x=8x \\ m_2=8 \end{gathered}`

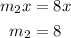
Since m1 ≠ m2, hence the lines are not parallel lines

Taking the product of the slopes to check if they are perpendicular;

`\begin{gathered} m_1\cdot m_2=(1)/(8)\cdot8 \\ m_1\cdot m_2=1 \end{gathered}`

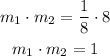
Since the product of the slopes is not -1, hence the lines are not perpendicular.

From the above explanation, we can see that both lines are neither parallel nor perpendicular. The slope of the lines are only reciprocal of each other