Question

Can you help me answer any of these I don't know where to start.

Answer 1

When a function is given in terms of some mathematical expression, its discontinuities can be found by analyzing the restrictions associated with the mathematical expression.

For instance, here are some of the restrictions that may be found:

The denominator of an expression must be different from 0.

A number should be positive in order to take its square root.

Take (a) as an example:

`f(x)=-(x)/(x^2+1)`

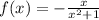
Since this expression involves a fraction, then the denominator x^2+1 should always be different from 0. To find the discontinuities, set the denominator equal to 0 and find which values of x make the denominator take that value:

`\begin{gathered} x^2+1=0 \\ \Rightarrow \\ x^2=-1 \end{gathered}`

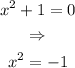
Since there is no real number such that it square is equal to -1, then there are no restrictions over that given function.

Take question (c) as another example:

`f(x)=-(x-4)/(x^2-16)`

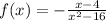
Since there is a fraction involved, set the denominator equal to 0:

`\begin{gathered} x^2-16=0 \\ \Rightarrow \\ x^2=16 \\ \Rightarrow \\ \sqrt[]{x^2}=\sqrt[]{16} \\ \Rightarrow \\ |x|=4 \\ \Rightarrow \\ x=\pm4 \end{gathered}`

Therefore, the points of discontinuity are -4 and 4.

For question (e):

`f(x)=-(|x|)/(x)`

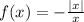
Since the denominator is equal to x, then we set it equal to 0:

`x=0`

And that is the only discontinuity point of this function.

In general, for these exercises, set the denominator equal to 0 and find the values of x that satisfy that condition.

The values which make the other denominators equal to 0, are:

(b)

`\begin{gathered} x=1 \\ x=-1 \end{gathered}`

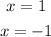
(d)

`\begin{gathered} x=\frac{-7+\sqrt[]{57}}{2} \\ x=\frac{-7-\sqrt[]{57}}{2} \end{gathered}`

(f)

`x=-3`