Question

Dilate the figure with the origin as the center of dilation.(x,y) → (0.8x,0.8y)

Answer 1

The coordinates of the vertices of the original figure are

A(5, 0), B(0, 5), C(-5, 0), and D(0, -5)

Therefore OB = 5, and OA = 5

Since AOB is a right-angled triangle with hypotenuse AB,

then

`AB^2=5^2+5^2=50`

Hence,

`AB=5\sqrt[]{2}`

From the graph, we can see that

BD = 10 =AC

and AC is perpendicular to BD

Therefore the figure is a square,

Which means that

`AB=BC=CD=DA=5\sqrt[]{2}`
`\begin{gathered} (x,y)\rightarrow(0.8x,0.8y) \\ \text{ is the same as} \\ (x,y)\rightarrow0.8(x,y) \end{gathered}`

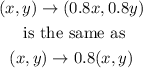
Hence the image of the figure under the transformation is also a square with the length of a side equal to the product of 0.8 and the length of side of a side of the original figure

That is

`\text{ length of each side of image =0.8}*5\sqrt[]{2}=4\sqrt[]{2}`

Therefore

`\begin{gathered} A^(\prime)B^(\prime)\text{ = 4}\sqrt[]{2} \\ B^(\prime)C^(\prime)\text{ = 4}\sqrt[]{2} \\ C^(\prime)D^(\prime)\text{ = 4}\sqrt[]{2} \\ D^(\prime)A^(\prime)\text{ = 4}\sqrt[]{2} \end{gathered}`