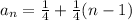Question

1/4, 2/4, 3/4, 4/4,... write a rule for the nth term of the sequence

Answer 1

You have the following sequence given in the exercise:

`(1)/(4),(2)/(4),(3)/(4),(4)/(4),\ldots`

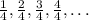
You can identify that it is an Arithmetic sequence, because the difference between one term and the previous one is always the same:

`\begin{gathered} (2)/(4)-(1)/(4)=(1)/(4) \\ \\ (3)/(4)-(2)/(4)=(1)/(4) \\ \\ (4)/(4)-(3)/(4)=(1)/(4) \end{gathered}`

By definition, you can express an Arithmetic sequence using a rule:

`a_n=a_1+d(n-1)_{}`

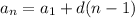
Where:

- The nth term of the sequence is

`a_n`

- The first term is

`a_1`

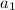
- The common difference is "d".

- The term position is "n".

In this case you know that:

`\begin{gathered} d=(1)/(4) \\ \\ a_1=(1)/(4) \end{gathered}`

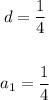
Therefore, you can substitute this value into

`a_n=a_1+d(n-1)_{}`

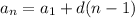
Then, you get that the answer is:

`a_n=(1)/(4)+(1)/(4)(n-1)`