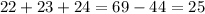We will have the following:
We will have to sum 3 consecutive numbers, so we will name those numbers:
n
n+1
n+2
and the fourth number n+3
We can see that they are consecutive since the sepatation is of 1 unit each, we will also have that they must follow:
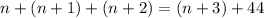
So, we solve for n:
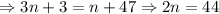
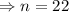
So, the three consecutive numbers are: 22, 23, & 24:
And we prove this by adding them and then subctacting 44 nd we should get 25: