Let's begin by listing out the information given to us:
time (t) = number of hours used
Company A: charges (A) = $40 per hour, equipment fee (e) = $175
Company B: charges (B) = $50 per hour, equipment fee (e) = $125
Equation 1

Equation 2

Let's proceed by equating both equation 2 & 1 to find the number of hours where they are equal
At what time interval is Company A is cheaper than Company B, we will represent it in inequality form:
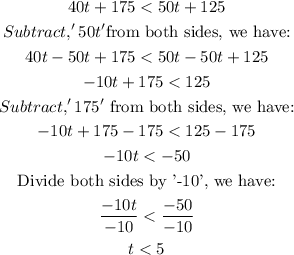
When the number of hours spent is more than 5 hours (>5), company A is cheaper than Company B