Question

Please help me with this homework question if possible, thank you!

Answer 1

The given problem can be exemplified in the following diagram:

To determine the total force we will determine the horizontal and vertical components of each of the forces.

For the 70 pounds force, we have that the horizontal component is:

`F_(70h)=70\sin 56`

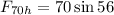
The vertical component is:

`F_(70v)=-70\cos 56`

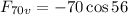
The negative sign is due to the fact that the vertical component is in the negative direction.

Now, we determine the horizontal component of the 50 pounds force:

`F_(50h)=50\sin 72`

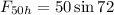
The vertical component is:

`F_(50v)=50\cos 72`

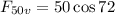
Now, we add the horizontal components:

`F_h=70\sin 56+50\sin 72`

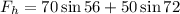
Solving the operations:

`F_h=105.59\text{ Pounds}`

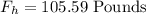
Now, we add the vertical components:

`F_v=-70\cos 56+50\cos 72`

Solving the operations:

`F_v=-23.69\text{ pounds}`

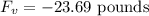
Now, the magnitude of the resulting force is given by the following formula:

`F=\sqrt[]{F^2_h+F^2_v}`

Plugging in the values we get:

`F=\sqrt[]{(105.59)^2+(-23.69)^2}`

Solving the operations:

`F=108.22\text{ pounds}`

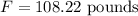
Therefore, the magnitude of the resulting force is 108.22 pounds.

To determine the angle of the resulting force we use the following formula:

`\theta=\tan ^(-1)((F_v)/(F_h))`

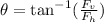
Plugging in the values we get:

`\theta=\tan ^(-1)(-(23.69)/(105.59))^{}`

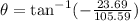
Solving the operations:

`\theta=-12.7\text{ degr}ees.\text{ }`

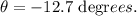
Therefore, the direction is -12.7°.