Question

A number is 10 more than another number twice the sum of the two numbers is 8. Find the two numbers Please help. Thanks

Answer 1

Let x and y be the unknown numbers.

We know that one number is 10 more than the other, this can be express as:

`y=x+10`

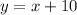
We also know that twice the sum of both numbers is equal to 8, the sum of the two numbers is:

`x+y`

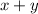
Twice this sum is:

`2(x+y)=2x+2y`

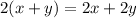
And this have to be equal to 8, then we have the equation:

`2x+2y=8`

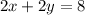
Hence we have the system of equations:

`\begin{gathered} y=x+10 \\ 2x+2y=8 \end{gathered}`

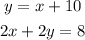
To solve this system we take the expression for y from the first equation and plug it in the second, then we solve for x:

`\begin{gathered} 2x+2(x+10)=8 \\ 2x+2x+20=8 \\ 4x+20=8 \\ 4x=8-20 \\ 4x=-12 \\ x=-(12)/(4) \\ x=-3 \end{gathered}`

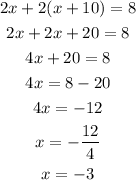
Now that we know the value of x we plug it in the expression for y:

`\begin{gathered} y=-3+10 \\ y=7 \end{gathered}`

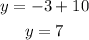
Therefore the numbers we are looking for are -3 and 7